Optics of Moving Sources
Problem 5.237
A narrow beam of electrons passes immediately over the surface of a metallic mirror with a diffraction grating with period \(d=2.0 \mu \mathrm{m}\) inscribed on it. The electrons move with velocity \(v\) comparable to \(c,\) at right angles to the lines of the grating. The trajectory of the electrons can be seen in the form of a strip, whose colouring depends on the observation angle \(\theta\) (Fig. 5.38). Interpret this phenomenon. Find the wavelength of the radiation observed at an angle \(\theta=45^{\circ}\).
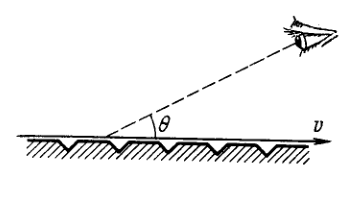
5.237. The charge of an electron and the positive charge induced in the metal form a dipole. In the reference frame fixed to the electron the electric dipole moment varies with a period \(T^{\prime}=d^{\prime} / v\) where \(d^{\prime}=d \sqrt{1-(v / c)^{2}}\). The corresponding "natural" frequency is \(v^{\prime}=v / d^{\prime} .\) Due to the Doppler effect the observed frequency is \[ v=v^{\prime} \frac{\sqrt{1-(v / c)^{2}}}{1-(v / c) \cos \theta}=\frac{v / d}{1-(v / c) \cos \theta} \] The corresponding wavelength is \(\lambda=c / v=d(c / v-\cos \theta) .\) When \(\theta=45^{\circ}\) and \(v \approx c\) the wavelength is \(\lambda \approx 0.6 \mu \mathrm{m}\)