Conductors and Dielectrics in an Electric Field
Problem 3.79
Near the plane surface of a uniform isotropic dielectric with permittivity the electric field strength in vacuum is equal to , the vector forming an angle with the normal of the dielectric's surface (Fig. 3.11). Assuming the field to be uniform both inside and outside the dielectric, find: (a) the flux of the vector through a sphere of radius with centre located at the surface of the dielectric: (b) the circulation of the vector around the closed path of length (see Fig. 3.11) whose plane is perpendicular to the surface of the dielectric and parallel to the vector .
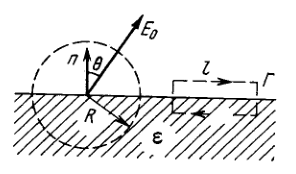
3.79. (a) (b)