All Problems

Conductors and Dielectrics in an Electric Field

Problem 3.78

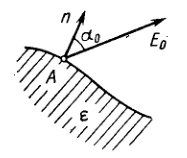
Near the point \(A\) (Fig. 3.10) lying on the boundary between glass and vacuum the electric field strength in vacuum is equal to \(E_{0}=10.0 \mathrm{~V} / \mathrm{m},\) the angle between the vector \(\mathbf{E}_ {0}\) and the normal n of the boundary line being equal to \(\alpha_{0}=30^{\circ} .\) Find the field strength \(E\) in glass near the point \(A,\) the angle \(\alpha\) between the vector \(\mathbf{E}\) and \(\mathbf{n},\) as well as the surface density of the bound charges at the point \(A\).

Reveal Answer
 3.78. E=E0εcos⁡2α0+ε2sin⁡2α0=5.2 V/mtan⁡α=εtan⁡α0, hence, α=74∘;σ′=ε0(ε−1)εE0cos⁡α0=64pC/m2\begin{aligned} &\text { 3.78. } E=\frac{E_{0}}{\varepsilon} \sqrt{\cos ^{2} \alpha_{0}+\varepsilon^{2} \sin ^{2} \alpha_{0}}=5.2 \mathrm{~V} / \mathrm{m}\\ &\tan \alpha=\varepsilon \tan \alpha_{0}, \text { hence, } \alpha=74^{\circ} ; \sigma^{\prime}=\frac{\varepsilon_{0}(\varepsilon-1)}{\varepsilon} E_{0} \cos \alpha_{0}=64 \mathrm{pC} / \mathrm{m}^{2} \end{aligned}
Prev
Next