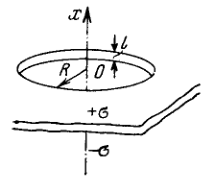
Problem 3.44

Two infinite planes separated by a distance \(l\) carry a uniform surface charge of densities \(\sigma\) and \(-\sigma\) (Fig. 3.7). The planes have round coaxial holes of radius \(R,\) with \(l \ll R .\) Taking the origin \(O\) and the \(x\) coordinate axis as shown in the figure, find the potential of the electric field and the projection of its strength vector \(E_{x}\) on the axes of the system as functions of the \(x\) coordinate. Draw the approximate plot \(\varphi(x)\).

\varphi=\frac{\sigma l}{2 \varepsilon_{0} \sqrt{x^{2}+R^{2}}}, E_{x}=-\frac{\sigma l R^{2}}{2 \varepsilon_{0}\left(x^{2}+R^{2}\right)^{3 / 2}} . \text { See Fig. }

Constant Electric Field in a Vacuum