Constant Electric Field in a Vacuum
Problem 3.43
Two coaxial rings, each of radius \(R,\) made of thin wire are separated by a small distance \(l(l \ll R)\) and carry the charges \(q\) and \(-q .\) Find the electric field potential and strength at the axis of the system as a function of the \(x\) coordinate (Fig. 3.6). Show in the same drawing the approximate plots of the functions obtained. Investigate these functions at \(|x| \gg R\)
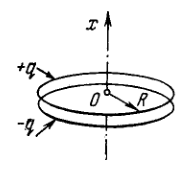
\begin{aligned} &\varphi=\frac{q l}{4 \pi \varepsilon_{0}} \frac{x}{\left(R^{2}+x^{2}\right)^{3 / 2}}, E_{x}=-\frac{q l}{4 \pi \varepsilon_{0}} \frac{R^{2}-2 x^{2}}{\left(R^{2}+x^{2}\right)^{5 / 2}}\\ &\text { where } \end{aligned} \(E_{x}\) is the projection of the vector \(\mathbf{E}\) on the \(x\) axis. The functions are plotted in Fig. 17. If \(|x| \gg R,\) then \(\varphi \approx \frac{q l}{4 \pi \varepsilon_{0} x^{2}}\) and \(E_{x} \approx \frac{q l}{2 \pi \varepsilon_{0} x^{3}}\)