Constant Magnetic Field, Magnetics
Problem 3.274
The magnetic induction in vacuum at a plane surface of a magnetic is equal to \(B\) and the vector \(B\) forms an angle \(\theta\) with the normal \(\mathrm{n}\) of the surface (Fig. 3.74\()\). The permeability of the magnetic is equal to \(\mu .\) Find: (a) the flux of the vector \(\mathbf{H}\) through the spherical surface \(S\) of radius \(R,\) whose centre lies on the surface of the magnetic; (b) the circulation of the vector \(\mathbf{B}\) around the square path \(\Gamma\) with side \(l\) located as shown in the figure.
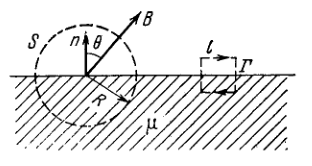
3.274. (a) \(\oint \mathbf{H} d \mathbf{S}=\pi R^{2} B \cos \theta \cdot(\mu-1) / \mu \mu_{0}\) (b) \(\oint \mathbf{B} d \mathbf{r}=(1-\mu) B l \sin \theta\)