All Problems

Electric Current

Problem 3.182

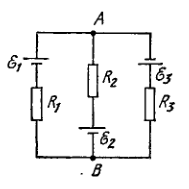
In the circuit shown in Fig. 3.45 the sources have emf's \(\mathscr{E}_ {1}=1.5 \mathrm{~V}, \quad \mathscr{E}_ {2}=2.0 \mathrm{~V}, \mathscr{E}{3}=2.5 \mathrm{~V},\) and the resistances are equal to \(R{1}=10 \Omega, R_{2}=20 \Omega, R_{3}=30 \Omega .\) The internal resistances of the sources are negligible. Find:

(a) the current flowing through the resistance \(R_{1}\) (b) a potential difference \(\varphi_{A}-\varphi_{B}\) between the points \(A\) and \(B\).

Reveal Answer
 3.182. (a) I1=[R3(E1−E2)+R2(E1+E3)]/(R1R2+R2R3++R3R1)=0.06 A;(b)φA−φB=E1−I1R1=0.9 V\begin{array}{r} \text { 3.182. (a) } I_{1}=\left[R_{3}\left(\mathscr{E}_{1}-\mathscr{E}_{2}\right)+R_{2}\left(\mathscr{E}_{1}+\mathscr{E}_{3}\right)\right] /\left(R_{1} R_{2}+R_{2} R_{3}+\right. \\ \left.+R_{3} R_{1}\right)=0.06 \mathrm{~A} ; \quad(\mathrm{b}) \varphi_{A}-\varphi_{B}=\mathscr{E}_{1}-I_{1} R_{1}=0.9 \mathrm{~V} \end{array}
Prev
Next