Problem 6.85

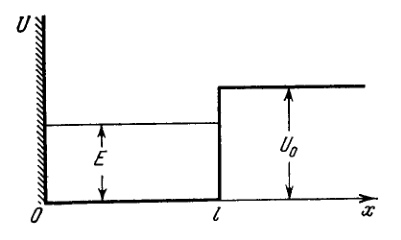
A particle of mass $m$ is located in a unidimensional potential field $U(x)$ whose shape is shown in Fig. $6.2,$ where $U(0)=\infty$. Find:

(a) the equation defining the possible values of energy of the particle in the region $E<U_{0}$; reduce that equation to the form $$\sin k l=\pm k l \sqrt{\hbar^{2} / 2 m l^{2} U_{0}}$$ where $k=\sqrt{2 m E / \hbar}$. Solving this equation by graphical means, demonstrate that the possible values of energy of the particle form a discontinuous spectrum; (b) the minimum value of the quantity $l^{2} U_{0}$ at which the first energy level appears in the region $E<U_{0} .$ At what minimum value of $l^{2} U_{0}$ does the $n$ th level appear?