Problem 5.71

Figure 5.14 illustrates the interference experiment with Fresnel mirrors. The angle between the mirrors is \(\alpha=12^{\prime},\) the distances from the mirrors' intersection line to the narrow slit \(S\) and the screen \(S c\) are equal to \(r=10.0 \mathrm{~cm}\) and \(b=130 \mathrm{~cm}\) respec tively. The wavelength of light is \(\lambda=0.55 \mu \mathrm{m} .\) Find: (a) the width of a fringe on the screen and the number of possible maxima; (b) the shift of the interference pattern on the screen when the slit is displaced by \(\delta l=1.0 \mathrm{~mm}\) along the arc of radius \(r\) with centre at the point \(O\); (c) at what maximum width \(\delta_{\max }\) of the slit the interference fringes on the screen are still observed sufficiently sharp.

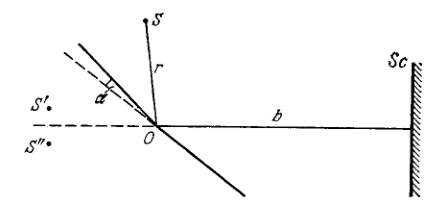
5.71. (a) \(\Delta x=\lambda(b+r) / 2 \alpha r=1.1 \mathrm{~mm}, 9\) maxima; (b) the shift is \(\delta x=(b / r) \delta l=13 \mathrm{~mm} ;\) (c) the fringe pattern is still sharp when \(\delta x \leqslant \Delta x / 2,\) hence \(\delta_{\max }=(1+r / b) \lambda / 4 \alpha=43 \mu \mathrm{m} .\)

Interference of Light