All Problems

Interference of Light

Problem 5.67

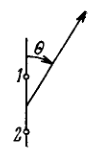
A system illustrated in Fig. 5.12 consists of two coherent point sources 1 and 2 located in a certain plane so that their dipole moments are oriented at right angles to that plane. The sources are separated by a distance \(d,\) the radiation wavelength is equal to \(\lambda\). Taking into account that the oscillations of source 2 lag in phase behind the oscillations of source 1 by \(\varphi(\varphi<\pi),\) find: (a) the angles \(\theta\) at which the radiation intensity is maximum; (b) the conditions under which the radiation intensity in the direction \(\theta=\pi\) is maximum and in the opposite direction, minimum.

Reveal Answer
 5.67. (a) cos⁡θ=(k−φ/2π)λ/d,k=0,±1,±2,…; (b) φ=π/2,d/λ=k+1/4,k=0,1,2,\begin{aligned} &\text { 5.67. (a) } \cos \theta=(k-\varphi / 2 \pi) \lambda / d, \quad k=0,\pm 1,\pm 2, \ldots ;\\ &\text { (b) } \varphi=\pi / 2, d / \lambda=k+1 / 4, k=0,1,2, \end{aligned}
Prev
Next