All Problems

Thermal Radiation. Quantum Nature of Light.

Problem 5.258

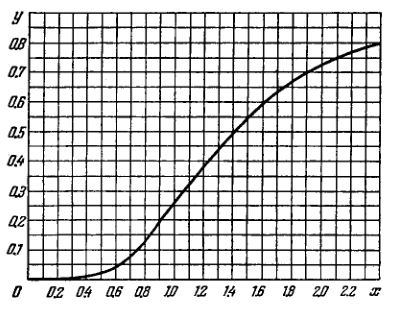
Fig. 5.40 shows the plot of the function \(y(x)\) representing a fraction of the total power of thermal radiation falling within the spectral interval from 0 to \(x\). Here \(x=\lambda / \lambda_{m}\left(\lambda_{m}\right.\) is the wavelength corresponding to the maximum of spectral radiation density). Using this plot, find: (a) the wavelength which divides the radiation spectrum into two equal (in terms of energy) parts at the temperature \(3700 \mathrm{~K}\); (b) the fraction of the total radiation power falling within the visible range of the spectrum \((0.40-0.76 \mu \mathrm{m})\) at the temperature \(5000 \mathrm{~K}\) (c) how many times the power radiated at wavelengths exceeding \(0.76 \mu \mathrm{m}\) will increase if the temperature rises from 3000 to \(5000 \mathrm{~K}\)

Reveal Answer
 (a) 1.1μm;(b)0.37;(c)P2/P1=(T2/T1)4(1−y2)/(1−y1)=4.9\text { (a) } 1.1 \mu \mathrm{m} ;(\mathrm{b}) 0.37 ;(\mathrm{c}) P_{2} / P_{1}=\left(T_{2} / T_{1}\right)^{4}\left(1-y_{2}\right) /\left(1-y_{1}\right)=4.9
Prev
Next