Polarization of Light
Problem 5.171
A narrow beam of light of intensity \(I_{0}\) falls on a planeparallel glass plate (Fig. 5.31 ) at the Brewster angle. Using the Fresnel equations, find: (a) the intensity of the transmitted beam \(I_{4}\) if the oscillation plane of the incident plane-polarized light is perpendicular to the incidence plane: (b) the degree of polarization of the transmitted light if the light falling on the plate is natural.
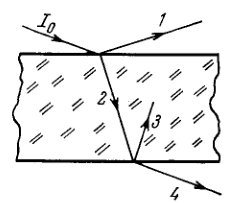
5.171. (a) In this case the coefficient of reflection from each surface of the plate is equal to \(\rho=\left(n^{2}-1\right)^{2} /\left(n^{2}+1\right)^{2},\) and therefore \(I_{4}=I_{0}(1-\rho)^{2}=16 \hat{I}_{0} n^{4} /\left(1+n^{2}\right)^{2}=0.725 I_{0}\) (b) \(P=\frac{1-\left(1-\rho^{\prime}\right)^{2}}{1+\left(1-\rho^{\prime}\right)^{2}}=\frac{\left(1+n^{2}\right)^{4}-16 n^{4}}{\left(1+n^{2}\right)^{4}+16 n^{4}} \approx 0.16,\) where \(\rho^{\prime}\) is the coeffic- ient of reflection for the component of light whose electric vector oscillates at right angles to the incidence plane.