Polarization of Light
Problem 5.165
Two parallel plane-polarized beams of light of equal intensity whose oscillation planes \(N_{1}\) and \(N_{2}\) form a small angle \(\varphi\) between them (Fig. 5.30) fall on a Nicol prism. To equalize the intensities of the beams emerging behind the prism, its principal direction \(N\) must be aligned along the bisecting line \(A\) or \(B\). Find the value of the angle \(\varphi\) at which the rotation of the Nicol prism through a small angle \(\delta \varphi \ll \varphi\) from the position \(A\) results in the fractional change of intensities of the beams \(\Delta I / I\) by the value \(\eta=100\) times exceeding that resulting due to rotation through the same angle from the position \(B\).
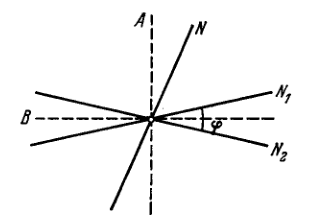
\(5.165 .\) The relative intensity variations of both beams in the cases \(A\) and \(B\) are \[ (\Delta I / I)_{A}=4 \cot (\varphi / 2) \cdot \delta \varphi, \quad(\Delta I / I)_{B}=4 \tan (\varphi / 2) \cdot \delta \varphi \] Hence \[ \eta=(\Delta I / I)_{A} /(\Delta I / I)_{B}=\cot ^{2}(\varphi / 2), \varphi=11.5^{\circ} \]