All Problems Diffraction of Light
Problem 5.143
The ultimate resolving power \(\lambda / \delta \lambda\) of the spectrograph's trihedral prism is determined by diffraction of light at the prism edges (as in the case of a slit). When the prism is oriented to the least deviation angle in accordance with Rayleigh's criterion, \[ \lambda / \delta \lambda=b|d n / d \lambda| \] where \(b\) is the width of the prism's base (Fig. 5.28\(),\) and \(d n / d \lambda\) is the dispersion of its material. Derive this formula.
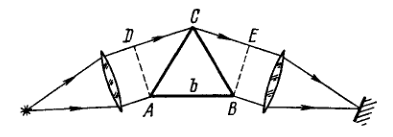
5.143. According to Rayleigh's criterion the maximum of the line of wavelength \(\lambda\) must coincide with the first minimum of the line of wavelength \(\lambda+\delta \lambda\). Let us write both conditions for the least deviation angle in terms of the optical path differences for the extreme rays (see Fig. 5.28): \[ b n-(D C+C E)=0, \quad b(n+\delta n)-(D C+C E)=\lambda+\delta \lambda_{\bullet} \] Hence, \(b \delta n \approx \lambda .\) What follows is obvious.