All Problems

Diffraction of Light

Problem 5.131

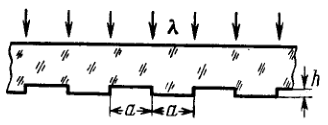
A plane light wave with wavelength \(\lambda\) falls normally on a phase diffraction grating whose side view is shown in Fig. 5.26 . The grating is cut on a glass plate with refractive index \(n\). Find the depth \(h\) of the lines at which the intensity of the central Fraunhofer maximum is equal to zero. What is in this case the diffraction angle corresponding to the first maximum?

Reveal Answer
 5.131. hk=λ(k−1/2)/(n−1), where k=1,2,…;asin⁡θ1=λ/2.\begin{array}{l} \text { 5.131. } h_{k}=\lambda(k-1 / 2) /(n-1), \quad \text { where } \quad k=1, \quad 2, \ldots ; \\ a \sin \theta_{1}=\lambda / 2 . \end{array}
Prev
Next