Diffraction of Light
Problem 5.102
A plane monochromatic light wave with intensity \(I_{0}\) falls normally on the surfaces of the opaque screens shown in Fig. 5.20. Find the intensity of light \(I\) at a point \(P\) (a) located behind the corner points of screens \(1-3\) and behind the edge of half-plane 4 ; (b) for which the rounded-off edge of screens \(5-8\) coincides with the boundary of the first Fresnel zone. Derive the general formula describing the results obtained for screens \(1-4 ;\) the \(\frac{14}{4^{1 / 3}}\) same, for screens \(5-8\).
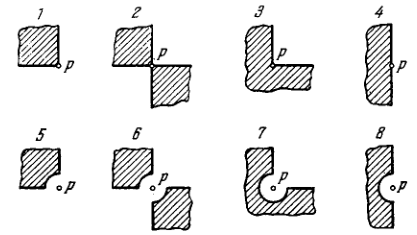
5.102. (a) \(I_{1} \approx \vartheta /{16} I_{0}, \quad I_{2}=1 / 4 I_{0}, I_{3}=1 /_{16} I_{0}, \quad I_{4}=I_{2}, \quad I \approx\) \(\approx(1-\varphi / 2 \pi)^{2} I_{0} ;\) (b) \(I_{5} \approx{ }^{25} /_{16} I_{0}, I_{6} \approx{ }^{9} / 4 I_{0}, I_{7} \approx{ }^{4} \rho /{16} I_{0}, \quad I_{8}=\) \(=I_{6}, I \approx(1+\varphi / 2 \pi)^{2} I_{0} .\) Here \(\varphi\) is the angle covered by the screen.