All Problems

Mechanical Oscillations

Problem 4.30

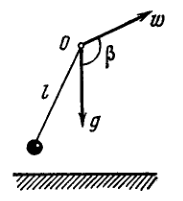
Find the period of small oscillations of a mathematical pendulum of length \(l\) if its point of suspension \(O\) moves relative to the Earth's surface in an arbitrary direction with a constant acceleration \(\mathbf{w}\) (Fig. 4.7). Calculate that period if \(l=21 \mathrm{~cm}, w=g / 2,\) and the angle between the vectors \(w\) and \(g\) equals \(\beta=120^{\circ}\).

Reveal Answer
 4.30. T=2πVl/∣g−w∣‾=0.8 s, where ∣g−w∣==g2+w2−2gwcos⁡β\begin{aligned} & \text { 4.30. } T=2 \pi V \overline{l /|\mathrm{g}-\mathbf{w}|}=0.8 \mathrm{~s}, \quad \text { where } &|\mathrm{g}-\mathbf{w}|=\\ =& \sqrt{g^{2}+w^{2}-2 g w \cos \beta} \end{aligned}
Prev
Next