Electromagnetic Waves. Radiation
Problem 4.218
A charged particle moves uniformly with velocity \(v\) along a circle of radius \(R\) in the plane \(x y\) (Fig. 4.40 ). An observer is located on the \(x\) axis at a point \(P\) which is removed from the centre of the circle by a distance much exceeding \(R\). Find: (a) the relationship between the observed values of the \(y\) projection of the particle's acceleration and the \(y\) coordinate of the particle; (b) the ratio of electromagnetic radiation flow densities \(S_{1} / S_{2}\) at the point \(P\) at the moments of time when the particle moves, from the standpoint of the observer \(P\), toward him and away from him, as shown in the figure.
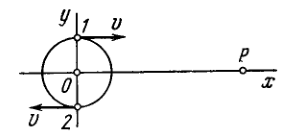
4.218. (a) Suppose that \(t\) is the moment of time when the particle is at a definite point \(x, y\) of the circle, and \(t^{\prime}\) is the moment when the information about that reaches the point \(P .\) Denoting the observed values of the \(y\) coordinate at the point \(P\) by \(y^{\prime}\) (see Fig. 4.40), we shall write \[ t^{\prime}=t+\frac{l-x(t)}{c}, \quad y^{\prime}\left(t^{\prime}\right)=y(t) \] The sought acceleration is found by means of the double differentiation of \(y^{\prime}\) with respect to \(t^{\prime}:\) \[ \frac{d y^{\prime}}{d t^{\prime}}=\frac{d y}{d t^{\prime}}=\frac{d y}{d t} \frac{d t}{d t^{\prime}}, \quad \frac{d^{2} y}{d t^{\prime 2}}=\frac{d t}{d t^{\prime}} \frac{d}{d t}\left(\frac{d y^{\prime}}{d t^{\prime}}\right)=\frac{v^{2}}{R} \frac{v / c-y / R}{(1-v y / c R)^{3}} \] where the following relations are taken into account: \(x=R \sin \omega t\) \[ y=R \cos \omega t, \text { and } \omega=v / R \] (b) Energy flow density of electromagnetic radiation \(S\) is proportional to the square of the \(y\) projection of the observed acceleration of the particle. Consequently, \(S_{1} / S_{2}=(1+v / c)^{4} /(1-v / c)^{4}\).