Electromagnetic Waves. Radiation
Problem 4.195
Proceeding from Maxwell's equations show that in the case of a plane electromagnetic wave (Fig. 4.38) propagating in vacuum the following relations hold:
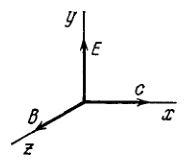
Proceeding from Maxwell's equations show that in the case of a plane electromagnetic wave (Fig. 4.38) propagating in vacuum the following relations hold:
