Constant Electric Field in a Vacuum
Problem 3.40
A point dipole with an electric moment \(p\) oriented in the positive direction of the \(z\) axis is located at the origin of coordinates. Find the projections \(E_{z}\) and \(E_{1}\) of the electric field strength vector (on the plane perpendicular to the \(z\) axis at the point \(S\) (see Fig. 3.4\()\). At which points is \(\mathbf{E}\) perpendicular to p?
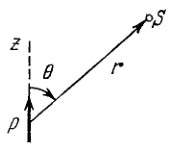
\[ \text { 3.40. } E_{z}=\frac{p}{4 \pi \varepsilon_{0}} \frac{3 \cos ^{2} \theta-1}{r^{3}}, E_{\perp}=\frac{p}{4 \pi \varepsilon_{0}} \frac{3 \sin \theta \cos \theta}{r^{3}} ; \] \(\mathbf{E} \perp \mathbf{p}\) at the points located on the lateral surface of a cone whose axis is directed along the \(z\) axis and whose semi-vertex angle \(\theta\) is found \begin{aligned} &\text { from the relation } \cos \theta=1 / \sqrt{3}\left(\theta_{1}=54.7^{\circ}, \theta_{2}=123.5^{\circ}\right) . \text { At these }\\ &\text { points } E=E_{\perp}=\frac{p \sqrt{2}}{4 \pi \varepsilon_{0} r^{3}} \end{aligned}