Problem 3.392

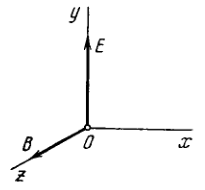
A particle with specific charge \(q / m\) moves in the region of space where there are uniform mutually perpendicular electric and magnetic fields with strength \(\mathbf{E}\) and induc-tion B (Fig. 3.104). At the moment \(t=0\) the particle was located at the point \(O\) and had zero velocity. For the non-relativistic case find: (a) the law of motion \(x(t)\) and \(y(t)\) of the particle; the shape of the trajectory; (b) the length of the segment of the trajectory between two nearest points at which the velocity of the particle turns into zero; (c) the mean value of the particle's velocity vector projection on the \(x\) axis (the drift velocity)