All Problems Electric Current
Problem 3.153
There is an infinite wire grid with square cells (Fig. 3.38). The resistance of each wire between neighbouring joint connections is equal to \(R_{0} .\) Find the resistance \(R\) of the whole grid between points \(A\) and \(B\). Instruction. Make use of principles of symmetry and superposition.
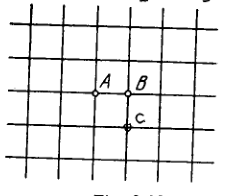
3.153. Imagine the voltage \(V\) to be applied across the points \(A\) and \(B .\) Then \(V=I R=I_{0} R_{0},\) where \(I\) is the current carried by the lead wires, \(I_{0}\) is the current carried by the conductor \(A B\). The current \(I_{0}\) can be represented as a superposition of two_currents. If the current \(I\) flowed into point \(A\) and spread all over] the infinite wire grid, the conductor \(A B\) would carry (because of symmetry) the current \(I / 4\). Similarly, if the current \(I\) flowed into the grid from infinity and left the grid through point \(B,\) the conductor \(A B\) would also carry the current \(I / 4\). Superposing both of these solutions, we obtain \(I_{0}=I / 2 .\) Therefore, \(R=R_{0} / 2 . \quad R_{A C}=\frac{2}{3} R_{0}\)