Problem 3.125

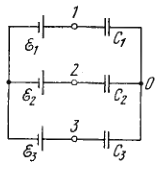
Determine the potential at point 1 of the circuit shown in Fig. 3.27 , assuming the potential at the point \(O\) to be equal to zero. Using the symmetry of the formula obtained, write the expressions for the potentials. at points 2 and 3 .

\begin{aligned} & \text { 3.125. } \varphi_{1}=\frac{\mathscr{E}_{2} C_{2}+\mathscr{E}_{3} C_{3}-\mathscr{E}_{1}\left(C_{2}+C_{3}\right)}{C_{1}+C_{2}+C_{3}} \\ \varphi_{2}=& \frac{\mathscr{E}_{1} C_{1}+\mathscr{E}_{3} C_{3}-\mathscr{C}_{2}\left(C_{1}+C_{3}\right)}{C_{1}+C_{2}+C_{3}}, \varphi_{3}=\frac{\mathscr{E}_{1} C_{1}+\mathscr{E}_{2} C_{2}-\mathscr{C}_{3}\left(C_{1}+C_{2}\right)}{C_{1}+C_{2}+C_{3}} \end{aligned}

Electric Capacitance, Energy of an Electric Field