All Problems Phase Transformations
Problem 2.204
Demonstrate that the straight line corresponding to the isothermal-isobaric phase transition cuts the Van der Waals isotherm so that areas and are equal (Fig. 2.5).
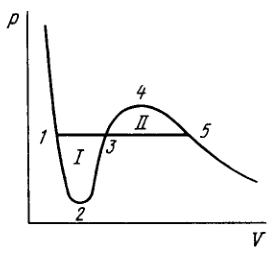
2.204. Let us apply Eq. (2.4e) to the reversible isothermic cycle Since the first two integrals are equal to zero, as well. The latter equality is possible only when areas and are equal. Note that this reasoning is inapplicable to the cycle for example. It is irreversible since it involves the irreversible transition at point 3 from a single-phase to a diphase state.