All Problems

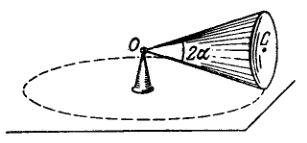
Kinematics

Problem 1.57

A round cone with half-angle \(\alpha=30^{\circ}\) and the radius of the base \(R=5.0 \mathrm{~cm}\) rolls uniformly and without slipping over a horizontal plane as shown in Fig. 1.8. The cone apex is hinged at the point \(O\) which is on the same level with the point \(C\), the cone base centre. The velocity of point \(C\) is \(v=10.0 \mathrm{~cm} / \mathrm{s} .\) Find the moduli of (a) the vector of the angular velocity of the cone and the angle it forms with the vertical; (b) the vector of the angular acceleration of the cone.

Reveal Answer
 (a) ω=v/Rcos⁡α=2.3rad/s,60∘, (b) β=(v/R)2tan⁡α==2.3rad/s2\text { (a) } \omega=v / R \cos \alpha=2.3 \mathrm{rad} / \mathrm{s}, 60^{\circ}, \text { (b) } \beta=(v / R)^{2} \tan \alpha= =2.3 \mathrm{rad} / \mathrm{s}^{2}
Prev
Next