All Problems

Kinematics

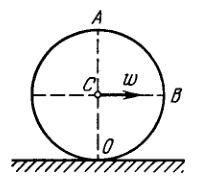
Problem 1.53

A ball of radius \(R=10.0 \mathrm{~cm}\) rolls without slipping down an inclined plane so that its centre moves with constant acceleration \(w=2.50 \mathrm{~cm} / \mathrm{s}^{2} ; t=2.00 \mathrm{~s}\) after the beginning of motion its position corresponds to that shown in Fig. 1.7. Find: (a) the velocities of the points \(A, B,\) and \(O\) (b) the accelerations of these points.

Reveal Answer
 (a) vA=2wt=10.0 cm/s,vB==2wt=7.1 cm/s,vo=0 (b) wA==2w1+(wt2/2R)2=5.6 cm/s2,wB==w1+(1−wt2/R)2=2.5 cm/s2,wO==w2t2/R=2.5 cm/s2\text { (a) } v_{A}=2 w t=10.0 \quad \mathrm{~cm} / \mathrm{s}, \quad v_{B}==\sqrt{2} w t=7.1 \quad \mathrm{~cm} / \mathrm{s}, \quad v_{o}=0 \text { (b) } w_{A}= =2 w \sqrt{1+\left(w t^{2} / 2 R\right)^{2}}=5.6 \mathrm{~cm} / \mathrm{s}^{2}, \quad w_{B}==w \sqrt{1+\left(1-w t^{2} / R\right)^{2}}=2.5 \mathrm{~cm} / \mathrm{s}^{2}, \quad w_{O}==w^{2} t^{2} / R=2.5 \mathrm{~cm} / \mathrm{s}^{2}
Prev
Next