Problem 1.51

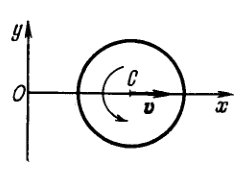
A rotating disc (Fig. 1.6) moves in the positive direction of the \(x\) axis. Find the equation \(y(x)\) describing the position of the instantaneous axis of rotation, if at the initial moment the axis \(C\) of the disc was located at the point \(O\) after which it moved (a) with a constant velocity \(v\), while the disc started rotating counterclockwise with a constant angular acceleration \(\beta\) (the initial angular velocity is equal to zero); (b) with a constant acceleration \(w\) (and the zero initial velocity), while the disc rotates counterclockwise with a constant angular velocity \(\omega\).