Relativistic Mechanics
Problem 1.353
The rod moves with a constant velocity relative to the rod (Fig. 1.91). Both rods have the same proper length and at the ends of each of them clocks are mounted, which are synchronized pairwise: with and with . Suppose the moment when the clock gets opposite the clock is taken for the beginning of the time count in the reference frames fixed to each of the rods. Determine: (a) the readings of the clocks and at the moment when they are opposite each other; (b) the same for the clocks and .
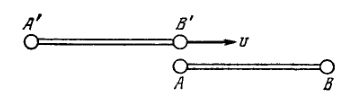
1.353. (a) (b)