All Problems

Elastic deformations

Problem 1.301

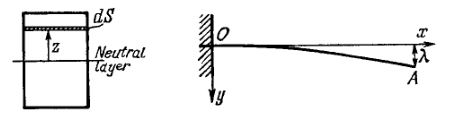
The bending of an elastic rod is described by the elastic curve passing through centres of gravity of rod's cross-sections. At small bendings the equation of this curve takes the form N(x)=EId2ydx2 N(x)=E I \frac{d^{2} y}{d x^{2}} where N(x)N(x) is the bending moment of the elastic forces in the crosssection corresponding to the xx coordinate, EE is Young's modulus, II is the moment of inertia of the cross-section relative to the axis passing through the neutral layer (I=∫z2dS,\left(I=\int z^{2} d S,\right. Fig. 1.75)\left.1.75\right)

Suppose one end of a steel rod of a square cross-section with side aa is embedded into a wall, the protruding section being of length ll (Fig. 1.76). Assuming the mass of the rod to be negligible, find the shape of the elastic curve and the deflection of the rod λ,\lambda, if its end AA experiences (a) the bending moment of the couple N0N_{0}; (b) a force FF oriented along the yy axis.

Reveal Answer
1.301. (a) Here NN is independent of xx and equal to N0.N_{0} . Integrating twice the initial equation with regard to the boundary conditions dy/dx(0)=0d y / d x(0)=0 and y(0)=0,y(0)=0, we obtain y=(N0/2EI)x2.y=\left(N_{0} / 2 E I\right) x^{2} . This is the equation of a parabola. The bending deflection is λ=\lambda= =N0l2/2EI,=N_{0} l^{2} / 2 E I, where I=a4/12I=a^{4} / 12 (b) In this case N(x)=F(l−x)N(x)=F(l-x) and y=(F/2EI)(l−x/3)x2y=(F / 2 E I)(l-x / 3) x^{2} λ=Fl3/3EI,\lambda=F l^{3} / 3 E I, where II is of the same magnitude as in (a).
Prev
Next