Dynamics of a solid body
Problem 1.280
A stationary platform P which can rotate freely about a vertical axis (Fig. 1.72) supports a motor and a balance weight . The moment of inertia of the platform with the motor and the balance weight relative to this axis is equal to I. A light frame is fixed to the motor's shaft with a uniform sphere rotating freely with an angular velocity about a shaft coinciding with the axis The moment of inertia of the sphere relative to the rotation axis is equal to Find: (a) the work performed by the motor in turning the shaft through ; through ; (b) the moment of external forces which maintains the axis of the arrangement in the vertical position after the motor turns the shaft through
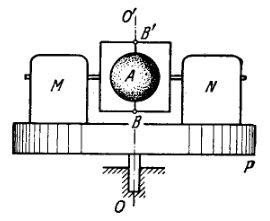
1.280. (a) (b)