Dynamics of a solid body
Problem 1.257
A spool with thread wound on it, of rests on a rough horizontal surface. Its moment of inertia relative to its own axis is equal to where is a numerical factor, and is the outside radius of the spool. The radius of the wound thread layer is equal to . The spool is pulled without sliding by the thread with a constant force directed at an angle to the horizontal (Fig. 1.63). Find: (a) the projection of the acceleration vector of the spool axis on the -axis; (b) the work performed by the force during the first seconds after the beginning of motion.
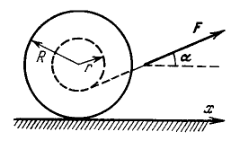
(a) (b)