All Problems

Laws of Conservation

Problem 1.146

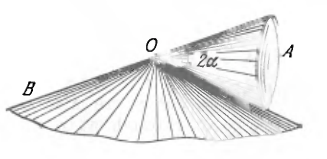
A round cone \(A\) of mass \(m=3.2 \mathrm{~kg}\) and halfangle \(\alpha=10^{\circ}\) rolls uniformly and without slipping along a round conical surface \(B\) so that its apex \(O\) remains stationary (Fig. 1.38). The centre of gravity of the cone \(A\) is at the same level as the point \(O\) and at a distance \(l=17 \mathrm{~cm}\) from it. The cone's axis moves with angular velocity \(\omega .\) Find: (a) the static friction force acting on the cone \(A\), if \(\omega=1.0 \mathrm{rad} / \mathrm{s}\) (b) at what values of \(\omega\) the cone \(A\) will roll without sliding, if the coefficient of friction between the surfaces is equal to \(k=0.25\)

Reveal Answer
<1.146.(a)Ffr=mg[sin⁡α+(ω2l/g)ccs⁡α]=6 Ng(k−tan⁡α)/l(1+ktan⁡α)=2rad/s (b) ω<\begin{aligned} &<\frac{1.146 .(a) F_{f r}=m g\left[\sin \alpha+\left(\omega^{2} l / g\right) \operatorname{ccs} \alpha\right]=6 \mathrm{~N}}{g(k-\tan \alpha) / l(1+k \tan \alpha)=2 \mathrm{rad} / \mathrm{s}}\\ &\text { (b) } \omega< \end{aligned}
Prev
Next