All Problems The Fundamental Equation of Dynamics
Problem 1.110
A sleeve \(A\) can slide freely along a smooth rod bent in the shape of a half-circle of radius \(R\) (Fig. 1.28 ). The system is set in rotation with a constant angular velocity \(\omega\) about a vertical axis \(O O^{\prime}\). Find the angle \(\theta\) corresponding to the steady position of the sleeve.
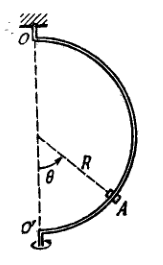
1.110. When \(\omega^{2} R>g\), there are two steady equilibrium positions: \(\theta_{1}=0\) and \(\theta_{2}=\arccos \left(g / \omega^{2} R\right) .\) When \(\omega^{2} \hat{R}<g\), there is only one equilibrium position: \(\theta_{1}=0 .\) As long as there is only one lower equilibrium position, it is steady. Whenever the second equilibrium position appears (which is permanently steady) the lower one becomes unsteady.